| Aufgabe 21 |
Gegeben ist ein kubisches Polynom p(x) mit den Nullstellen
x1, x2,
x3, das
folgender Bedingung genügt: 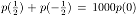 .
Welchen Wert nimmt dann der Term .
Welchen Wert nimmt dann der Term 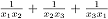 an? an?
(Australian Mathematical Olympiad, 1996)
|
| Aufgabe 22 |
Die quadratische Gleichung 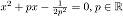 hat die Nullstellen a, b. Zeige:
hat die Nullstellen a, b. Zeige: 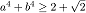 . .
(1992 Telecom Junior Contest)
|
| Aufgabe 23 |
Bestimme die Lösungsmenge der Gleichung (x + 1998)(x + 1999)(x + 2000)(x + 2001) + 1 = 0.
(Australian Mathematical Olympiad, 1998)
|
| Aufgabe 24 |
Es ist zu zeigen, daß die Gleichung
x4 + 131 = 3y4 keine
ganzzahligen Lösungen x, y haben kann.
(Australian Mathematical Olympiad, 1984)
|
| Aufgabe 25 |
Gesucht sind alle Funktionen 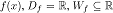 , welche
der Funktionalgleichung
f(u + v)f(u - u) = 2u + f(u2 - v2) genügen.
Dabei sind u, v reelle Zahlen. , welche
der Funktionalgleichung
f(u + v)f(u - u) = 2u + f(u2 - v2) genügen.
Dabei sind u, v reelle Zahlen.
(Australian Intermediate Contest, 1996)
|