Unbestritten besteht die Absicht der Zeitschrift Wurzel im
Verbreiten und Fördern von Mathematik. Das ist auf unterschiedlichen
Wegen möglich. So kann der Leser Beiträge aus verschiedenen
mathematischen Sachgebieten durcharbeiten und dabei sein Wissen erweitern.
Unter der Rubrik Wurzel – Aufgaben wird er zudem
angeregt, ausgewählte Aufgaben und Probleme zu lösen.
„Mathematik betreiben” umfaßt aber noch mehr. So wurde und wird von
vielen mathematisch tätigen Personen die Auffassung vertreten, daß nicht
nur das Auffinden von Lösungen zu bestehenden Fragen, sondern auch und gerade
das Suchen neuer Fragestellungen und deren Bearbeitung als Kernelement
mathematischen Arbeitens zählt. Beispielsweise bedeuten für Albert
Einstein gerade die Fähigkeiten
- neue Fragen zu stellen,
- neue Möglichkeiten zu eröffnen,
- alte Probleme aus einem neuen Blickwinkel zu sehen,
wirklichen Fortschritt in der Wissenschaft (vgl. [1], S. 246).
Akzeptiert man die Sichtweise, ist es naheliegend und sinnvoll, diesem
produktiven Aspekt von Mathematik auch in der Wurzel
entsprechend Aufmerksamkeit zu schenken. Das im folgenden Beschriebene soll
dahingehend einen Beitrag leisten.
Ich werde nun eine mathematische Problemstellung bzw. Thematik vorstellen
und sie dann zum weiteren Erschließen, Entwickeln, Ausbauen etc. für
die Leser „freigeben”.
Vor geraumer Zeit fand ich in [2], S. 13 folgende elementare
Problemstellung:
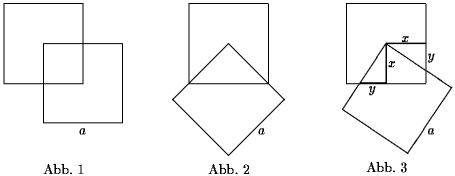
Zwei zueinander kongruente Quadrate liegen so übereinander, daß eine
Ecke des oben liegenden gleichzeitig Mittelpunkt des unten liegenden
ist.
Was kann man über den gemeinsamen Flächeninhalt aussagen?
Bezeichnet man die Seitenlänge der Quadrate mit a, dann ist der
gemeinsame Flächeninhalt A stets a²/4.
Für die in den Abb. 1 und 2 dargestellten zwei Spezialfälle
läßt sich der Flächeninhalt auf verschiedenen Wegen sehr
einfach bestimmen. Auch für den allgemeinen Fall gibt es mehrere
Möglichkeiten, A = a²/4 zu beweisen.
In Abb. 3 sind die Hilfslinien x und y eingefügt.
Sie sind jeweils Katheten eines rechtwinkligen Dreiecks. Diese Dreiecke können
durch Drehung ineinander überführt werden und sind damit kongruent.
Daher kann das Flächenstück, welches abgeschnitten wurde,
an anderer Stelle wieder angesetzt werden, so daß als gemeinsame
Fläche nun wieder die des ersten Spezialfalls vorliegt.
Diese Problemstellung ist in verschiedene Richtungen ausbaufähig. Unter
anderem gibt es folgende Variationsmöglichkeiten:
- Variationen hinsichtlich der Art der Figuren (z. B. nicht mehr
Quadrate oder nicht mehr zueinander kongruente Figuren …)
- Variationen hinsichtlich der Dimension (z. B. Betrachtungen im Raum)
- Variationen hinsichtlich des Drehpunktes (z. B. nicht mehr
„Mittelpunkt” der unten liegenden Fläche)
- Variationen hinsichtlich der Fragestellung (z. B. ist nicht mehr der
gemeinsame Inhalt zu betrachten).
Das ist freilich nur ein kleiner Ausschnitt denkbarer Arbeitsrichtungen. Mir
sind weiterführende Arbeiten von verschiedenen Personen zu dem oben
genannten Ausgangsproblem bekannt. Darauf möchte ich aber nicht weiter
eingehen, sondern vielmehr die Wurzel-Leser
aufrufen, sich selbst Anschlußprobleme auszuwählen bzw.
zu suchen und daran zu arbeiten. Die jeweiligen Arbeitsergebnisse können
der Wurzel zugesandt werden.
Es ist vorgesehen, verschiedene ausgewählte Einsendungen in einem
Wurzel-Heft zu publizieren.
Mit dieser Aufgabenstellung soll ein breites Spektrum von Lesern
angesprochen werden. Ich vertrete die Meinung, daß es geeignete
Anschlußprobleme sowohl für Schüler als auch für
Hochschullehrer der Mathematik gibt.
Es wäre schön, würden viele Leser dem Aufruf folgen, sich mit
der Thematik auseinandersetzen und ihre Arbeitsergebnisse der
Wurzel zusenden.
Viel Spaß, Freude und Erfolg!
Literaturverzeichnis
- [1]
-
Schönpflug, W. / Schönpflug, U.:
Psychologie.
Psychologie Verlagsunion. München 1989.
- [2]
- Zimmermann, B.: Problemlösen als eine Leitidee für den Mathematikunterricht.
Erschienen in: MU, Heft 3/1983. Klett Verlag. Stuttgart 1983.
|
